各企業や学校では、患者の推移を見ながら、通常勤務を戻すのを「いつ」にするのか、登校再開を「いつ」にするのか、頭を悩ませていることだろう。他の企業の動向や、政府の発表を頼りにしていることだと思う。しかし、独自に判定したい方もいるだろう。その一つの方法として、公開されているデータを活用して、現在の患者数の増減を、もう少し数学的に理解する方法を説明しようと思う。

微分を離散データにも使おう

　そのためには、高校の数学で習う、微分を活用する。まず、以下の式を考えたい。

　この式を、実際にグラフにしたものが、以下である。

　青い点線（値は左の軸を参照）が、この式の図になる。1階微分というグラフ（値は右の軸を参照）があるが、今は理解しなくても良い。高校の数学を習った人は計算できるだろう。実際には以下のような式になる。

この式を、中学生で習った因数分解を使うと、以下のように変形出来る。

この式の特徴は、xが、10と20の時に、y=0になることである。実際に上記のグラフの赤い曲線は、そのようになっている。

そして、2階微分（値は右の軸を参照）は、以下のような式になる。

この1階微分と2階微分の値が、プラス（正）か、マイナス（負）かで、青色のグラフの増減の説明が可能である。

1階微分の正・負は、関数（y)の増・減を説明している。そして、2階微分の正・負は、グラフの傾きが、「急」・「ゆっくり」を示している。

この知識をCovid 19の患者数ので使おう

　この考えは、Covid 19の患者数という離散データでも使える。ここでは、東京都が公開している「都内の最新感染動向」のデータを使い、都内の患者数のデータをグラフにしてみた。

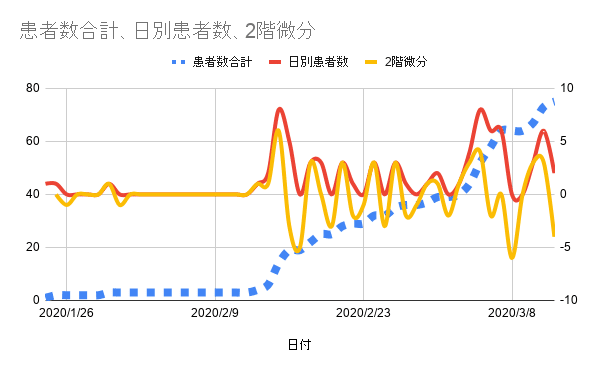
青が、患者数（左軸を参照）である。1階微分は、患者の増加数（赤い線・右軸を参照）であり、上記の「日別患者数）である。2階微分（黄色の線・右軸を参照）は、日別患者数の増加数で求めることができる。実際の現象では、数式のようにきれいな曲線になることは少なく、上記のようにバタバタとしたデータになることが多い。

　患者は増加しているのであるが、望ましいのは患者の増加がゆっくりになることであろう。それは、1階微分（日別患者数）が正で、2階微分が負となる場合である。このグラフでは、黄色の2階微分は正になった負になったりしており、その回数もほぼ同じであり、明らかに増加がゆっくりになっているとは言えないのである。

　このように、公開されているデータと、高校の数学でデータ分析が可能であるのだ。